Arquímedes mostró de nuevo su habilidad para los cálculos numéricos en estación aproximada
de la razón de una circunferencia a su diámetro. Partiendo del exageno regular
inscrito en la circunferencia, calcula Arquímedes los perímetros de los
polígonos obtenidos duplicados sucesivamente el número de lados hasta llegar al
polígono regular de 96 lados. El procedimiento interactivo que utiliza para
estos polígonos está relacionado con lo que a veces se llama el algoritmo de Arquímedes.
Consideremos la sucesión
son respectivamente los perímetros de los
polígonos regulares circunscrito e inscrito de n lados, comenzando con el
tercer término de la sucesión podemos calcular cualquier termino a partir de
los dos anteriores tomando alternativamente sus medidas armónica y geométrica.
Es decir,
Etcétera. Si uno lo prefiere, puede proceder de una manera alternativa
utilizando la sucesión han, A n, a 2 n, A 2 n…, donde a n y A n son
respectivamente el área de los polígonos regulares inscrito de n lados.
Entonces el tercer término y los sucesivos se obtienen tomando alternativa la
media geométrica y armónica, de tal manera que:
Etcétera.
El método de Arquímedes para calcular raíces cuadradas al terminar el perímetro
del exógeno
circunscrito y para hallar medidas geométricas era muy semejante al que
utilizaban los babilonios. El resultado final de los cálculos de Arquímedes
sobre el círculo fue una aproximación al valor de π expresada por la desigualdad
lo que suponía una estimación sensiblemente mejor que la de los
egipcios y los babilonios. (Debe tenerse en cuenta claramente que ni Arquímedes
ni ningún otro matemático griego utilizo nunca ni nuestra notación π ni la idea
de un numero como razón de la circunferencia al diámetro de un circulo). Este
resultado aparece en la posición 3 del tratado sobre la medida del círculo, una
de las obras más importantes de Arquímedes durante la edad media. Esta obrita,
probablemente incompleta tal como ha llegado a nosotros, incluye solo 3
proposiciones, de las que una se reduce a la demostración por el método de
exhausción. De que el área del círculo es igual a la de un triángulo rectángulo
que tenga como uno de sus catetos la circunferencia del círculo y el otro igual
al radio.
Es improbable que fuera Arquímedes el descubridor de este teorema,
puesto que ya se supone en la cuadratura del círculo atribuida a Dinostrato.

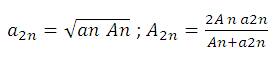


No hay comentarios.:
Publicar un comentario